Understanding Transformer Self-Attention 💬

Date: September 5, 2023

This article is a work in progress

Self attention is the underlying principle of the Transformer architecture.

Before reading this article, you should have an understanding of:

• Basic neural networks
• Text Embedding/ Word2Vec
• RNN's

Self-attention is a mechanism that allows each token in a sequence to dynamically weigh and aggregate information from all other tokens in that sequence.

More simply, self-attention controls how much each word in a sentence should “pay attention” to the other words in the sentence.

Here's an over-simplified demonstration of what self attention does:

Cats like to lie in the evening sun. ⇒ linking subject and verb (high attention score for “Cats” and “lie”)

Cats like to lie in the evening sun. ⇒ linking subject and main verb (high attention score for “Cats” and “like”)

Cats like to lie in the evening sun. ⇒ linking preposition and noun (high attention score for “in” and “sun”)

---

Self attention solves the vanishing gradient, and non-parallelizability problems inherent to RNN’s.

In Transformers, each token proportionately, and in-parallel, ‘attends’ to all other tokens in the sequence.

This contrasts with RNNs, where context is sequentially accumulated and passed to the next consecutive unit, leading to information loss as the sequence lengthens and inability to parallelize training.

More simply, self attention acts on the whole input at once, while RNN’s process the input word by word.

Embedding the Input Sequence

This sentence will be used as the input sequence:

I think therefore I am

The input sequence needs to be turned into a list of embeddings.

Each of the 5 tokens (words) of the sequence will be represented by a 2-dimensional embedding. For the sake of brevity, a randomly initialized tensor will be used as a proxy to an Embedding layer.

Initializing the (5,2) matrix to represent the input text:

T,C = 5,2 #declare the Time, and Channel sizes
X = torch.Embedding(T,C) #initialize the tensor with random values

T, and C define the shape of the input data:

• T: Time (or Sequence Length). This indicates the length of the sequence;
• C: Channels (or Features). This refers to the feature size for each token in the sequence. In the context of a language model, this is the embedding dimension.

Returns:

tensor([[ 0.9188,  0.0800],
        [ 1.3041, -0.0827],
        [ 0.2717, -1.2120],
        [ 0.1656, -0.8852],
        [ 1.6164,  0.3943]])

Adding Positional Embeddings

To also provide information about the position of each token in the sequence, a positional embedding is added to each token embedding. Positional embeddings consist of a predictable consecutive pattern, usually from sine and cosine waves.

The positional embedding vector consists of alternating sine and cosine values:

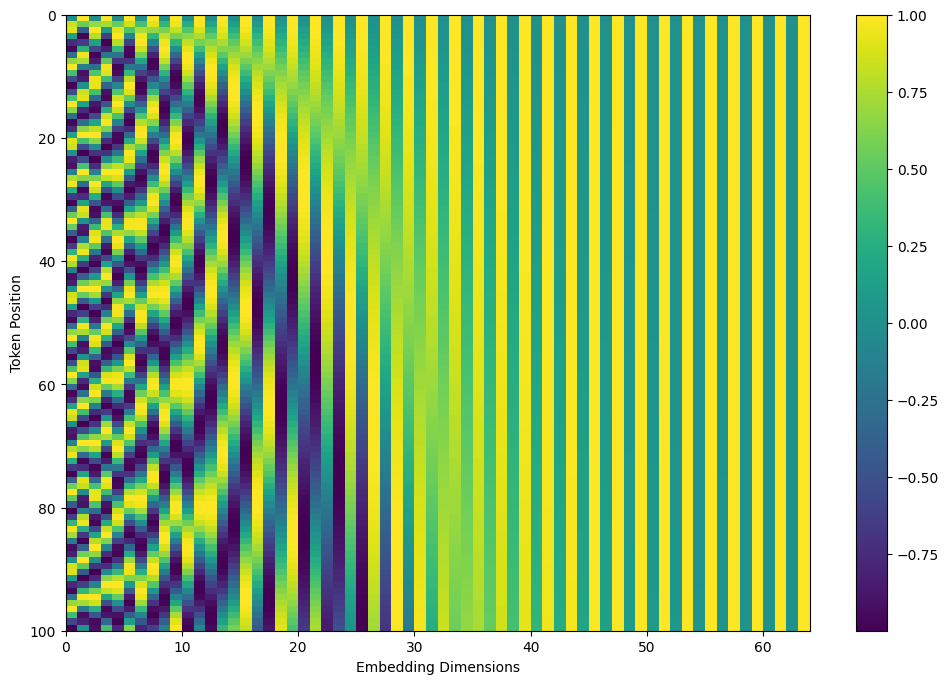
Each token will get a positional embedding the same size as its token embedding.

The positional embeddings for the sequence will have the same (T,C) shape as the input matrix:

tensor([[[ 0. 1. ],
		[ 0.84147098 0.54030231],
		[ 0.90929743 -0.41614684],
		[ 0.14112001 -0.9899925 ],
		[-0.7568025 -0.65364362]]])

X = X + positional_embeddings

This is the approach used in modern transformers, but this can also be substituted with a standard learned Embedding table.

Now that the input sequence is embedded and has positional information added, it is ready to be passed into the attention layers.

Deriving the Key, Query, and Value Matrices

Key- summary of who I am as a token Query- what am I looking for in other tokens Value- the information I will share with other tokens

At the core of an attention head are the Key (K), Query (Q), and Value (V) layers. These are used to learn the contextual relationships between tokens.

They are derived by multiplying the input with the K, Q and V weight matrices (the equivalent of linear layers, without a bias):

$K=X{W}_K$

$$Q=X{W}_Q$$$$V=X\ast W_V$$$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

Where:

• Q is the matrix of Queries
• K is the matrix of Keys
• V is the matrix of Values
• $d_k$ is the dimension of the keys (usually the model's embedding size divided by the number of attention heads)

The term $\frac{Q{K}^T}{\sqrt{d_k}}$calculates the dot product of the queries and keys. The result is then scaled down by the square root of the depth (or dimension) of the key, $d_k$, to prevent the softmax from squashing its inputs too much, especially when the embeddings become large. The softmax is applied over the keys for each query.

The output of the softmax is the attention weights, which are then used to take a weighted sum of the values.

Calculating the Attention Scores

Attention is a measure of relevance between tokens. To calculate this score, the $K$ and $Q$matrices are multiplied together:

$AttentionScores=K\ast Q$

Aggregating the Token Information

Creating the Lower Triangular Matrix (Decoder-only Transformer):

tril = torch.tril(torch.ones(T,T))

tensor([[1., 0., 0., 0., 0.],
        [1., 1., 0., 0., 0.],
        [1., 1., 1., 0., 0.],
        [1., 1., 1., 1., 0.],
        [1., 1., 1., 1., 1.]])

Here a lower triangular matrix is initialized.

tril is a lower triangular matrix of size T x T filled with ones in the lower triangle and zeros in the upper triangle.

In self-attention, each token in a sequence has the potential to attend to every other token in the same sequence, including itself. This "attending" determines how much each token should be influenced by every other token.

Imagine a sequence of length T. For a given token:

• We need a weight indicating how much it should attend to the 1st token.
• We need another weight for how much it should attend to the 2nd token.
• ...
• We need a weight for how much it should attend to the Tth token.

So for just one token, we need T weights. Since there are T tokens in the sequence, and each of those tokens needs T weights, there are T×T weights in total.

2. Initializing the Attention Weights:

wei = torch.zeros((T,T))

wei is initialized as a T x T matrix of zeros. It will be used to store the attention weights, indicating how much each token should attend to every other token.

3. Masking Future Tokens:

wei = wei.masked_fill(tril == 0, float('-inf'))

tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
        [0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
        [0., 0., 0., -inf, -inf, -inf, -inf, -inf],
        [0., 0., 0., 0., -inf, -inf, -inf, -inf],
        [0., 0., 0., 0., 0., -inf, -inf, -inf],
        [0., 0., 0., 0., 0., 0., -inf, -inf],
        [0., 0., 0., 0., 0., 0., 0., -inf],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

The idea behind attention is that when considering a particular token, we decide how much to "attend" to or "focus" on other tokens. In causal or autoregressive models, it's important that a token doesn't attend to future tokens (tokens that come after it), as this would be using information from the future.

To ensure this, we use the masked_fill function. For positions where tril is zero (indicating future tokens in the upper triangle), we set the corresponding position in wei to negative infinity (float('-inf')). This ensures that after applying the softmax function, the attention weight for future tokens becomes zero.

4. Softmax for Normalizing the Attention Weights:

wei = F.softmax(wei, dim=1)

tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.5000, 0.5000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.3333, 0.3333, 0.3333, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.2500, 0.2500, 0.2500, 0.2500, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.2000, 0.2000, 0.2000, 0.2000, 0.2000, 0.0000, 0.0000, 0.0000],
        [0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.0000, 0.0000],
        [0.1429, 0.1429, 0.1429, 0.1429, 0.1429, 0.1429, 0.1429, 0.0000],
        [0.1250, 0.1250, 0.1250, 0.1250, 0.1250, 0.1250, 0.1250, 0.1250]])

The softmax function is applied to the wei matrix row-wise (with dim=1). After softmax, the values in each row will sum to 1. Due to the negative infinity values we added in the previous step, any future token positions will have an attention weight of nearly 0, ensuring no attention is given to future tokens.

5. Applying Attention:

xbow3 = wei @ x

tensor([[[-0.8273,  0.5410],
         [-0.5045,  0.0594],
         [ 0.3320,  0.6988],
         [-0.0415,  0.5347],
         [ 0.3069,  0.8687],
         [-0.0678,  0.6424],
         [-0.0256,  0.4929],
         [-0.0346,  0.4638]],

        [[ 0.4554, -0.0601],
         [ 0.3639, -0.3632],
         [ 0.3842, -0.1176],
         [ 0.8112,  0.2629],
         [ 0.7386,  0.5212],
         [ 0.7461,  0.1248],
         [ 0.6825,  0.1393],
         [ 0.4978,  0.1053]],

        [[ 0.4904, -0.1202],
         [ 0.4504, -0.0612],
         [ 0.4384, -0.4280],
         [ 0.5894, -0.6804],
         [ 0.3690, -0.5270],
         [ 0.3813, -0.5088],
         [ 0.0388, -0.4376],
         [-0.1165, -0.2274]],

        [[-0.6851,  0.0906],
         [-1.3416, -0.0507],
         [-0.6536, -0.0603],
         [-0.4225, -0.1353],
         [-0.2528, -0.2319],
         [-0.0375, -0.0600],
         [-0.2067, -0.1786],
         [-0.3234, -0.1669]]])

The matrix multiplication here aggregates the information from the input sequences (x) based on the attention weights (wei).

For each token, it computes a weighted sum of all previous tokens (including itself) in the sequence based on the attention weights. The attention weights dictate how much each token should contribute to this sum.

Relation to Self-Attention:

The mechanism here is a simplified, illustrative version of self-attention. In actual self-attention mechanisms, like those in the Transformer model, the attention weights (wei in this example) are learned from the data and depend on the token embeddings themselves. Specifically, they are computed based on dot products between query, key, and value vectors derived from the token embeddings.

This implementation demonstrates the foundational idea of weighing tokens differently based on their positions and relative importance. It also showcases the principle of not allowing tokens to attend to future tokens, a common approach in autoregressive models.